Saltar la navegación

Repaso

Objetivo

El alumno retomará las técnicas del cálculo integral mediante la realización de ejercicios, técnicas que son fundamentales para encontrar soluciones de los sistemas dinámicos.

Instrucciones:

  • Lea cuidadosamente lo que le solicita la actividad.
  • Tenga a la mano su formulario.
  • Identifique los datos proporcionados.
  • Determine la respuesta correcta a cada ejercicio de acuerdo al algoritmo de solución.
  • Compruebe la solución en caso de conocer el método apropiado.
  • En caso de ser necesario realice el procedimiento en hojas blancas y entregue a su profesor.

Criterios de Evaluación:

No aplica.

Actividad

El teorema fundamental del cálculo indica que las operaciones de diferenciación e integración son operaciones inversas, por lo que la utilización del cálculo diferencial es de vital importancia para entender el concepto de integral y para poder realizar los algoritmos de integración en algunos métodos de integración, por ello es necesario realizar un breve repaso de las derivadas más sencillas a fin de recordar el uso de los formularios.

Ejercicio 1. Realice las siguientes derivadas por el método que más se le facilite.

a)  k) 

b) 

 l) 

c) 

 m) 
d)  n) 
e)  ñ) 
f)  o) 
g)  p) 
h)  q) 
i) 
 r) 
j) 
 s) 

Ejercicio 2. Integrales Directas.

La forma más sencilla de realizar integrales es a partir de funciones que son idénticas a las proporcionadas por los formularios o que únicamente requieren un arreglo algebraico, este tipo de integrales se llaman integrales directas: 

a)  o) 
b)  p) 
c)  q) 
d)  r) 
e)  s) 
f)  t) 
g)  u) 
h)  v) 
i)  w) 
j)  x) 
k)  y) 
l)  z) 
m)  aa) 
n)  ab) 
ñ) 

Ejercicio 3. Integrales por cambio de variable o sustitución.

Este tipo de integrales son aquellas en las que es necesario agrupar un conjunto de elementos y sustituir este conjunto de elementos por una nueva variable, con el fin de poder realizar una integración directa.

El cambio de variable se realiza de la siguiente forma, y depende del tipo de función que se desea integrar:

Forma de la función

Nueva variable

a)División

Denominador

b)Potencia

Base de la potencia

c)Funciones trascendentes

Argumento

a)  i) 
b)  j) 
c)  k) 
d)  l) 
e) 
f) 
g)   
h) 

Ejercicio 4. Realice las siguientes integrales:

a) 
b) 
c) 
d) 
e) 
f) 
g) 
h) 
i) 
j) 

Ejercicio 5. Realice las siguientes integrales mediante el método de integración por partes:

a) 
b) 
c) 
d) 
e) 

Ejercicio 6. Determine el valor de las siguientes integrales mediante el método de fracciones parciales simples:

a) 
b) 
c) 
d) 
e) 

Ejercicio 7. Resuelva las siguientes integrales definidas. utilice el método que más se le facilite:

a)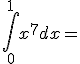 
b)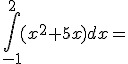 
c)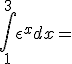 
d)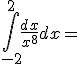 
e)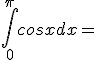 

Ejercicio 8. Determine el área bajo las curvas siguientes, en el dominio señalado. Es necesario realizar la gráfica de cada área calculada indicando el intervalo que cubre el área:

a) 
b) 
c) 
d) 
e)